This post briefly describes the problem of probabilistic planning, and explains in informal terms what makes a planning problem probabilistically interesting, along with some examples.

Primer on probabilistic planning

In a nutshell, planning is about finding a way to win, and as such, the field of research on planners is vast. However, there is no single textbook definition of “planning”, so in this post I’ll try to be as general as possible. One description of a planning problem could be: given a description of an environment, find a sequence of actions that brings the environment from the initial state of the environment to a goal state. There are multiple ways to describe the environment: for example in formal logic with the situation calculus, or more commonly as a Markov decision process (MDP). In probabilistic planning problems, the functions describing the MDP are not necessarily deterministic: executing action $a$ in state $s$ will bring the environment to state $s'$ with a probability of $T(s,a,s')$. In contrast with the control problem of reinforcement learning, where the goal is to find an optimal policy (i.e. a mapping from states to actions), in planning one is interested only in a partial policy that brings the agent closer to a goal state, or frequently only a single action that brings the agent closer to a goal state from the current state. An example planning problem is thus: “Siri, show me a way to the library.” Then Siri responds either with a plan that I can follow from the first step to the last (i.e. a route from start to finish), or only an action that I can take right now (“go forward 100 meters”).

Graphical representation of an example MDP:

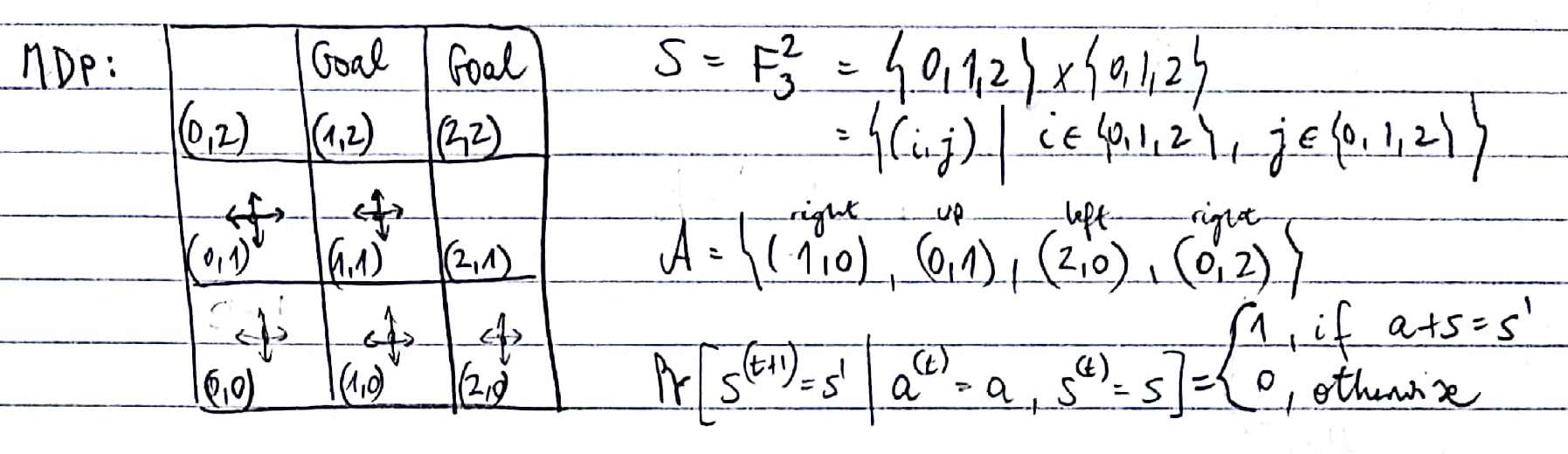
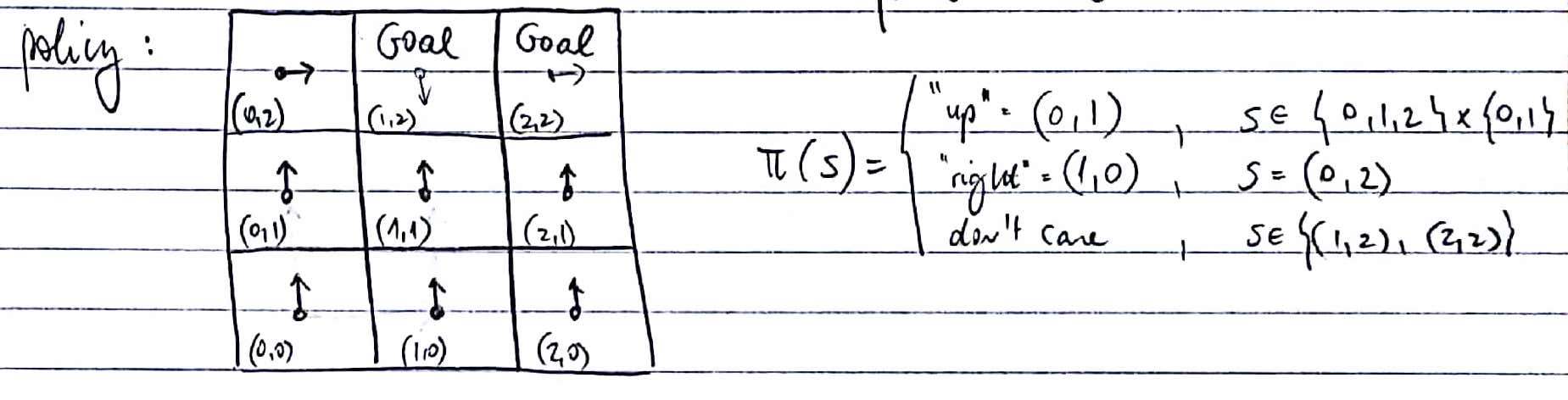
An example policy for the same MDP:

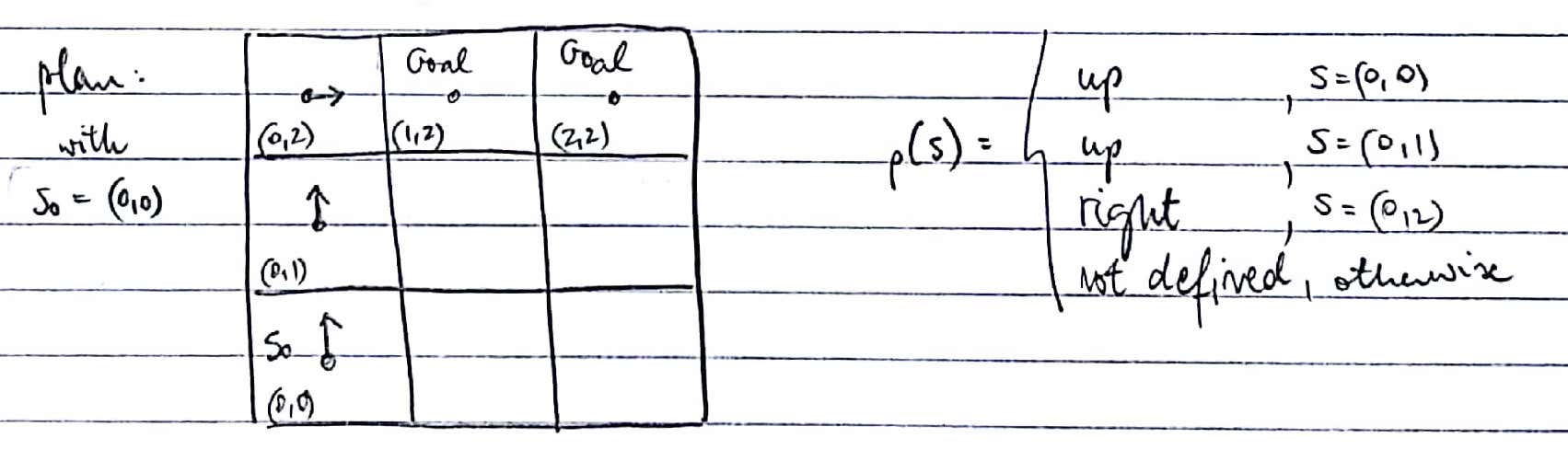
An example plan for the same MDP:

The approach taken by a planner differs based on the discounting factor \$\gamma \$ and the distribution of rewards. In a shortest path problem the future rewards are discounted (\$0 < \gamma < 1 \$), and there might be a constant negative reward for every step taken. Together with a positive reward in goal states, an agent with the goal of maximizing return – i.e. the sum of discounted expected future rewards – has incentives to minimize the length of the path to the goal. However, if there is no discounting (\$\gamma = 1 \$) and there’s a positive reward only in the goal states, it is sufficient for the agent to find any way to the goal. (Some call these goal-based problems (Yoon, Fern, Givan, & Kambhampati, 2008).) In the next section we’ll see that not all plans are created equal, so even in the non-discounted case we want one that ends up in a goal state with the highest probability.

In an offline approach to deterministic planning problems, a planner is given an environment, initial state and goal state, and it needs to return a sequence of actions that brings the environment to the goal state. However, this offline approach does not work for probabilistic problems, where the outcome of an action is not always in our control. Hence a probabilistic planner is usually executed online: it makes an observation (e.g. the current state of the environment, in the fully observable case), does some magic, and outputs a single action that brings the agent closer to a goal state. Nature brings the agent to a new state, not necessarily the one you desired, and these steps are repeated, until you run out of time or end up at a goal.

Since the fourth International Planning Competition in 2004 hosted by the ICAPS (International Conference on Automated Planning and Scheduling), this event featured a probabilistic track. The winner of IPPC 2004 was FF-Replan, a planner that simplifies the probabilistic planning problem into a deterministic one by not considering the multiple potential effects of an action (Yoon, Fern, & Givan, 2007) – hence the title of the paper, “FF-Replan: A Baseline for Probabilistic Planning.”

Probabilistically interesting planning problems

Iain Little and Sylvie Thiébaux analyzed the common characteristics of planning problems that can and cannot be optimally solved by a planner like FF-Replan (Little & Thiébaux, 2007). They gave necessary and sufficient conditions for a probabilistic planning problem to be probabilistically interesting: on a problem fulfilling these conditions, a planner that determinizes the problem will lose crucial information, and will do worse than a probabilistic planner. In this section I’ll summarize these conditions using natural language, slightly diverging from the vocabulary of the paper. For formal definitions and more examples, see the original paper; it is an interesting read.

Criterion 1: there are multiple paths from the start to the goal. If there is only a single path, then any planner that finds a path will do equally good, as this will be the only one.

Counterexample:

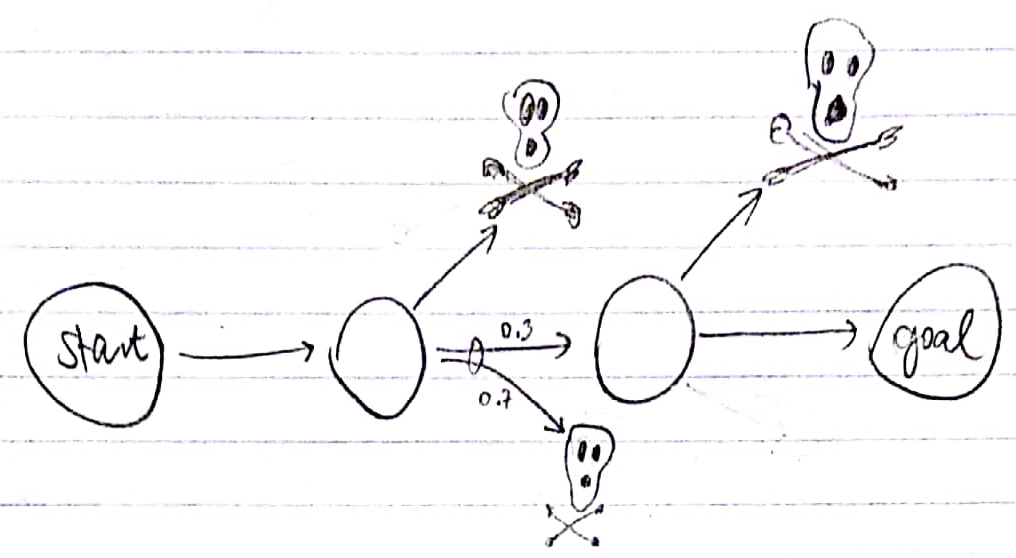
Criterion 2: where the above two paths diverge, there is a choice about which way to go, i.e. a state \$s_{crossroads}\$ from which action \$a_1\$ leads to one road with a different probability than action \$a_2\$ does. (Yes, this is a sufficient condition for the first criterion.) If it’s only luck that separates the two paths, then the agent doesn’t have much of a choice to do better.

Counterexample:

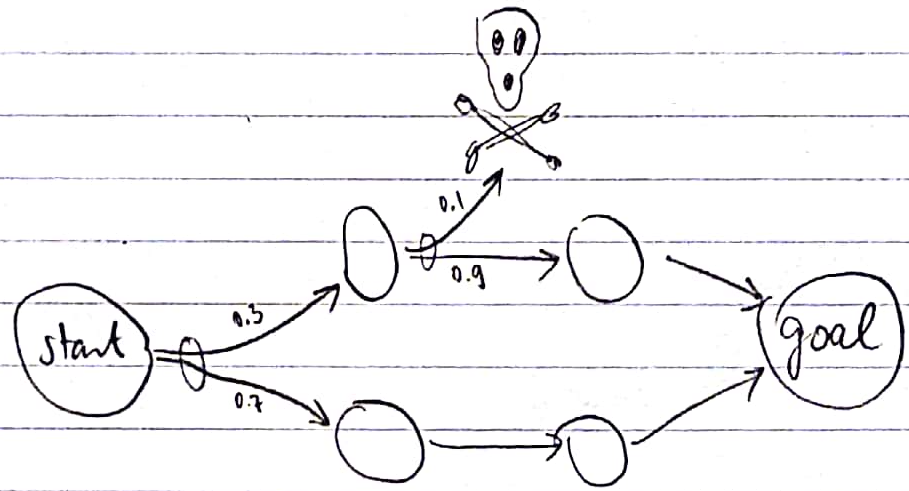
Criterion 3: there must be a non-trivially avoidable dead end in the environment. A dead end is an absorbing state that is not a goal state, i.e. a state from which there is no path to any goal state. For a dead end to be avoidable, there must be a state \$s_{crossroads}\$ with at least two possible actions \$a_{deadly}\$ and \$a_{winning}\$, such that executing \$a_{deadly}\$ brings the agent to the dead end with a higher probability than executing \$a_{winning}\$. A dead end is non-trivially avoidable if \$s_{crossroads}\$ is on a path from the initial state to a goal state, and there is a non-zero chance of reaching a goal state after executing either \$a_{winning}\$ or \$a_{deadly}\$.

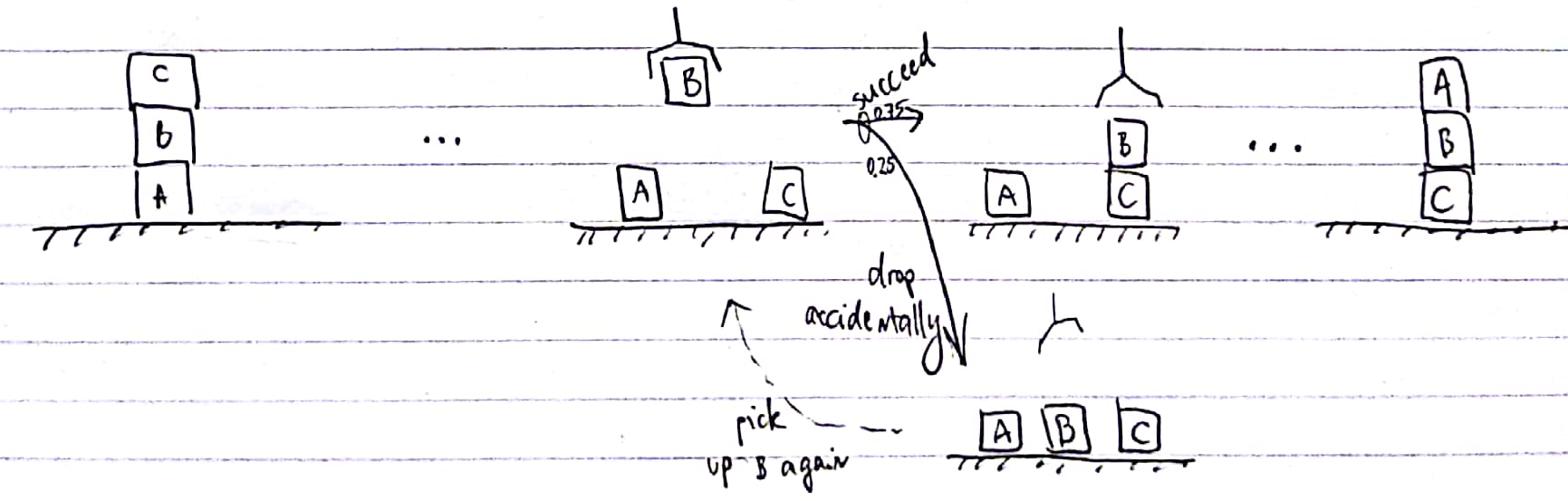
Counterexample: the probabilistic version of Blocksworld, where the worst case scenario is that a block is dropped accidentally, does not contain dead ends; the environment is irreducible. (This was an actual problem of IPPC 2004.)

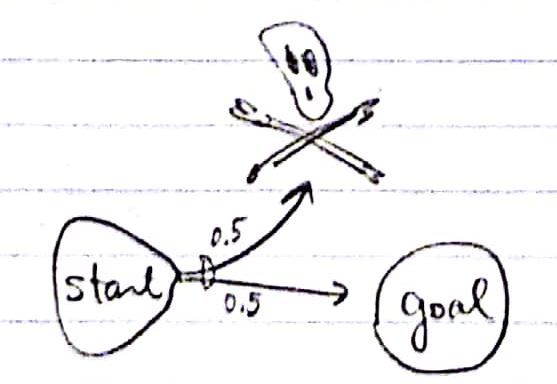
Counterexample: all dead ends are unavoidable.

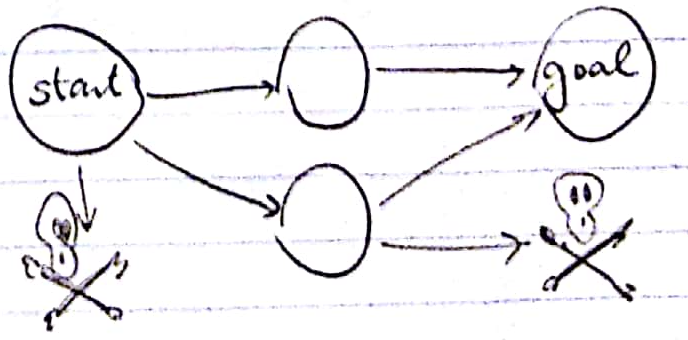
Counterexample: all dead ends are trivially avoidable.

A simple yet “interesting” planning problem

A very simple problem that is probabilistically interesting is what the authors call climber, described by the following story:

You are stuck on a roof because the ladder you climbed up on fell down. There are plenty of people around; if you call out for help someone will certainly lift the ladder up again. Or you can try to climb down without it. You aren’t a very good climber though, so there is a 40% chance that you will fall and break your neck if you do it alone. What do you do?

Graphical representation of the climber problem:

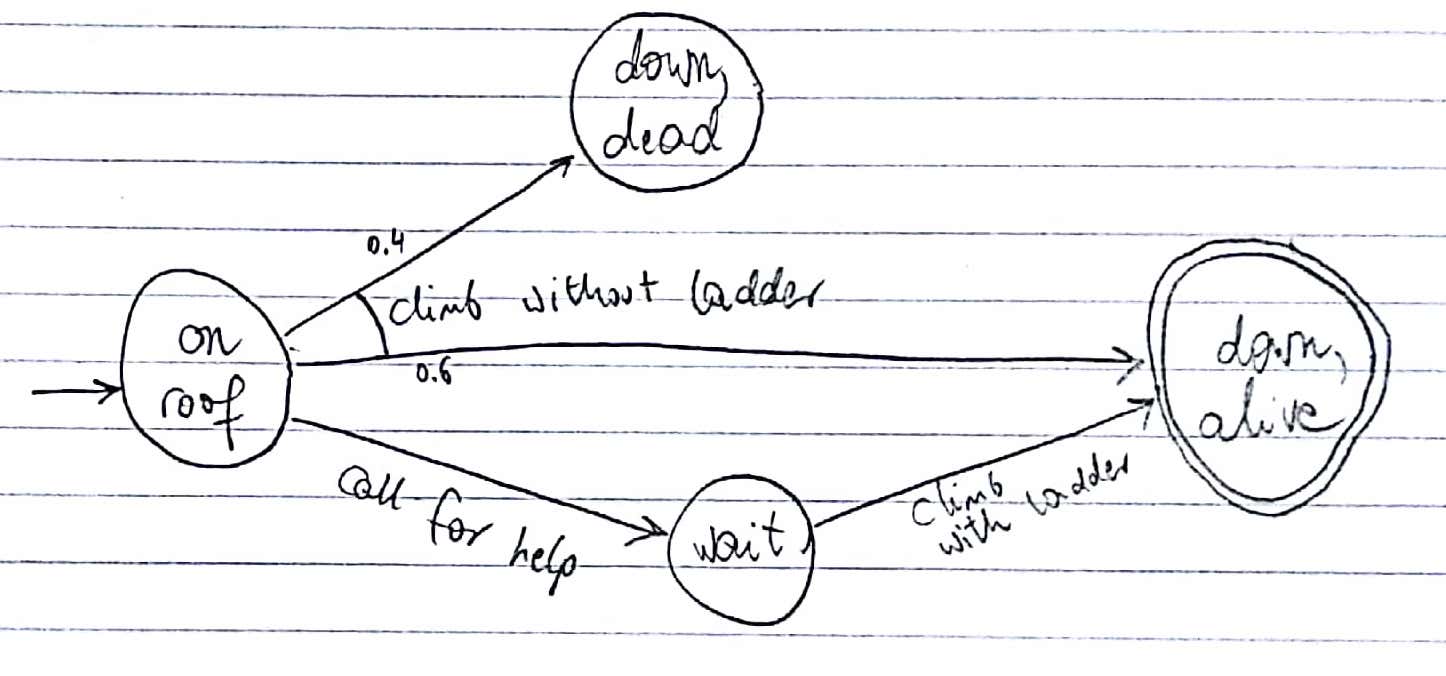
Despite the simplicity of this problem, most methods to turn it into a deterministic problem fail. Little and Thiébaux described 3 ways to determinize a problem, and they called a resulting deteministic problem a “compilation”.

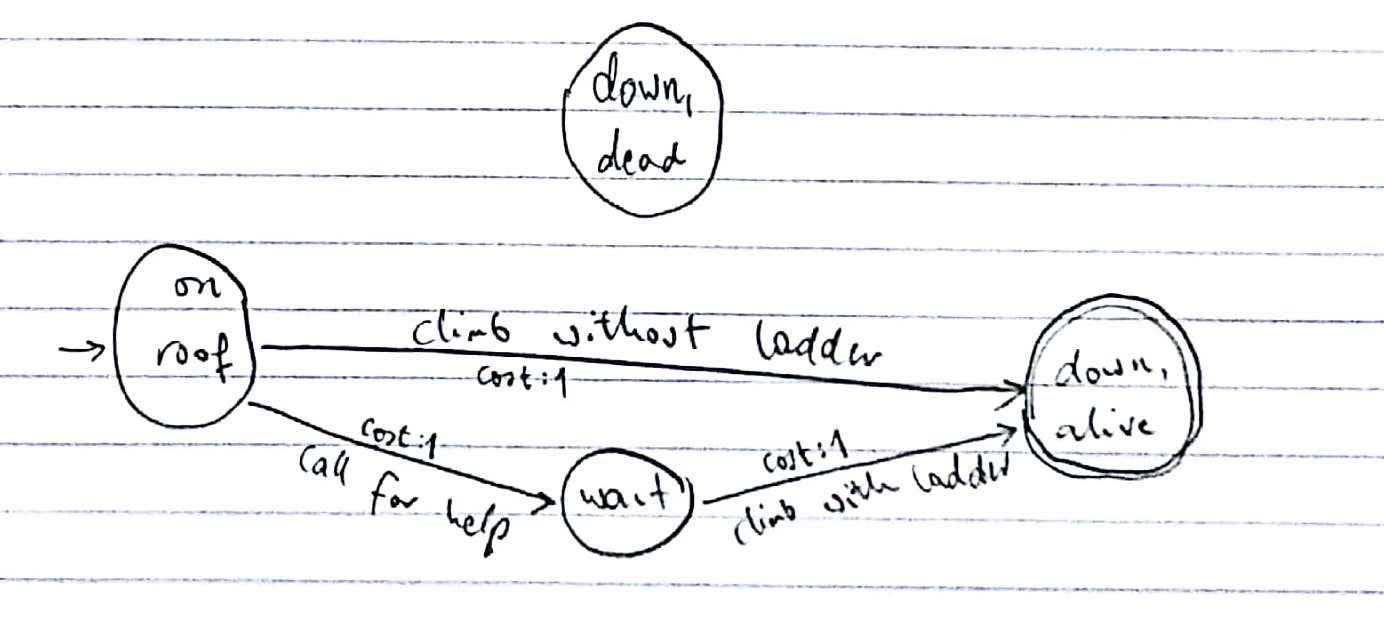
The REPLAN1 approach simply drops all but the most likely outcome of every action, and finds the shortest goal trajectory. (This was the approach used by FF-Replan.) Compilation of the climber problem according to REPLAN1:

REPLAN2(shortest) turns every possible probabilistic outcome of an action into the outcome of a deterministic action, each with a cost of 1. Optimizing for smallest cost thus finds the shortest goal trajectory, but this might not be the one with the highest success probability. Compilation of the climber problem according to REPLAN2(shortest):

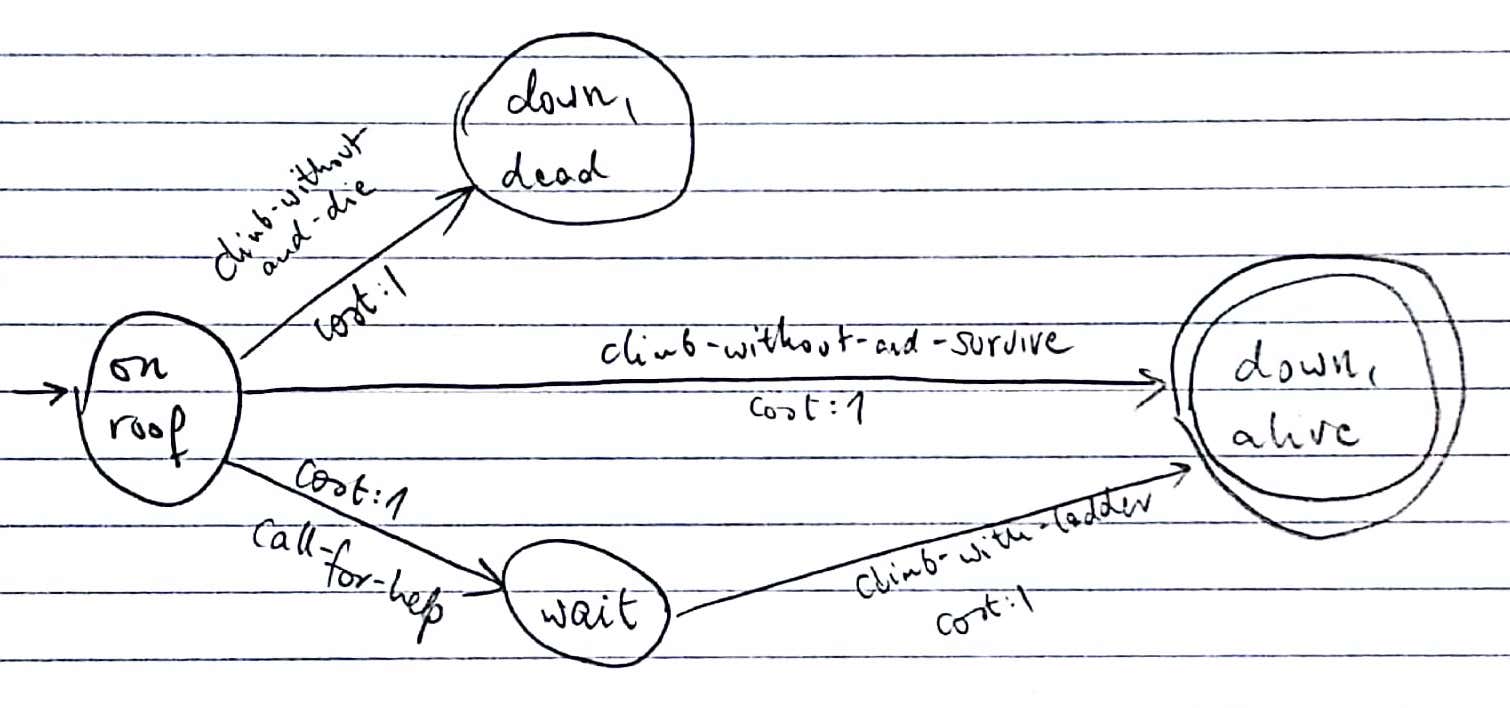
REPLAN2(most-likely) also turns every outcome into a separate deterministic action, but the new action costs are the negative log probability of the relevant outcome. This is the only compilation of the problem that finds the optimal path for climber, but for many other problems even this one will be suboptimal. The resulting compilation is as follows:

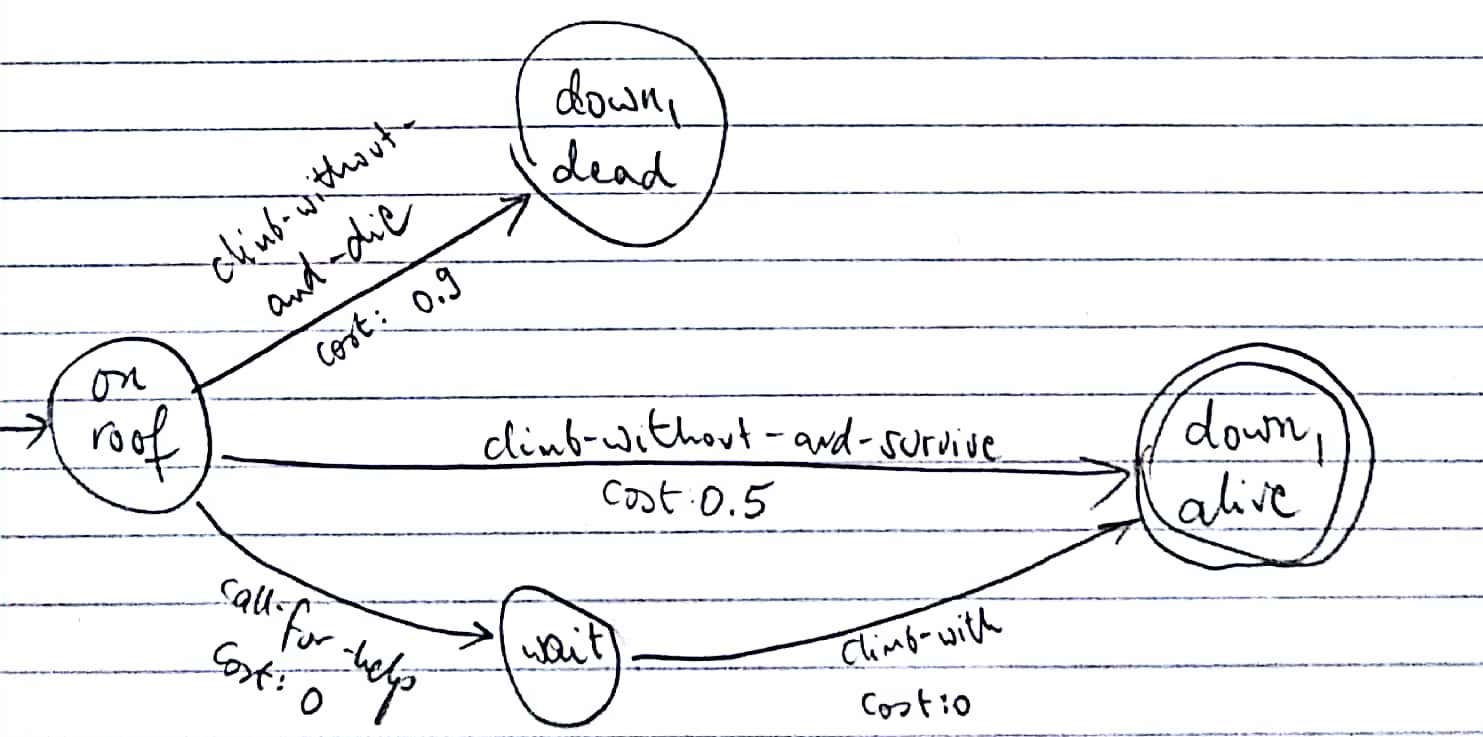
Summary

Finding the optimal goal trajectory in a probabilistic planning problem is computationally expensive, so most planners use some heuristics. One way to plan in a stochastic environment is to change the probabilistic planning problem into a deterministic shortest path problem and replan after (almost) every step, which is computationally efficient, but in many cases suboptimal. This article outlined the attributes of probabilistically interesting problems, where the deterministic replanning approach often fails. As such, recent probabilistic planners use more complicated methods (or often a portfolio of probabilistic planners), but replanners remain a good baseline to compare against.

References

1. Little, I., & Thiébaux, S. (2007). Probabilistic planning vs. replanning. Workshop, ICAPS 2007. Retrieved from http://users.cecs.anu.edu.au/ iain/icaps07.pdf
2. Yoon, S. W., Fern, A., & Givan, R. (2007). FF-Replan: A Baseline for Probabilistic Planning. In M. S. Boddy, M. Fox, & S. Thiébaux (Eds.), Proceedings of the Seventeenth International Conference on Automated Planning and Scheduling, ICAPS 2007, Providence, Rhode Island, USA, September 22-26, 2007 (p. 352). AAAI. Retrieved from http://www.aaai.org/Library/ICAPS/2007/icaps07-045.php
3. Yoon, S. W., Fern, A., Givan, R., & Kambhampati, S. (2008). Probabilistic Planning via Determinization in Hindsight. In D. Fox & C. P. Gomes (Eds.), Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence, AAAI 2008, Chicago, Illinois, USA, July 13-17, 2008 (pp. 1010–1016). AAAI Press. Retrieved from http://www.aaai.org/Library/AAAI/2008/aaai08-160.php